Ficha 37 en PDF
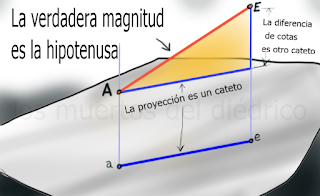
1 Si el segmento es paralelo a un plano de proyección se ve directamente (IO), pero si no es así, podemos usar la diferencia de cotas o alejamientos para hallar la verdadera magnitud.
2
3Podemos ver la verdadera magnitud de AE por diferencia de cotas, y, alargando la hipotenusa, conseguir la distancia que buscamos.
5En este caso si se ve directamente.6
4. La distancia entre un punto y un plano no proyectante no se ve directamente. Así que 1- Trazamos por el punto una recta perpendicular al plano. 2- Hallamos la intersección de la recta con el plano (E). El segmento AE es la distancia. 3-Por diferencia de cotas hallamos la solución.
38 DISTANCIAS II
1 Al ser proyectante, todos los puntos que distan 2cms del plano se ven directamente. Así que nos basta con hacer una paralela a 20mm.2 Aquí se ve la distancia también directamente.3 Este plano es perpendicular al perfil.
4 El cuadrado definiría un plano proyectante vertical (no es necesario dibujarlo). Tras hallar el centro de cuadrilátero, trazamos dos semirrectas perpendiculares al plano y cuadrado.En el vertical podemos medir directamente la altura. Llevamos la cota del vértice a la proyección horizontal. Dibujamos las aristas de la pirámide, distinguiendo partes vistas y ocultas.
5. También es proyectante el plano, así que lo vemos directamente6 1- Hallamos el plano: No hacen falta las trazas, se ve directamente que es proyectante. 2-Dibujamos semirrectas perpendiculares al plano. La medida se ve directamente en el P.V.Unimos los puntos 39 DISTANCIAS III
Ficha 39 en PDF
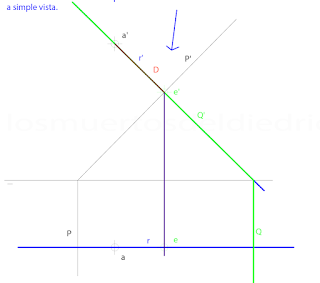
1 La distancia entre una recta y un punto será un segmento perpendicular. Para hallarlo trazamos un plano perpendicular a la recta que contenga a A.
En este caso 1º Dibujamos un plano perpendicular a R que contiene a A,plano Q (frontal).2º Hallamos la sección que Q produce en R (se vé directamente: punto E). 3º La distancia es el segmento AE, que se ve en verdadera magnitud en el PV. Es tan fácil que podríamos razonarlo y hallar la distancia directamente.
2. En este caso la recta es perpendicular al perfil, así que allí podemos ver directamente las distancias.3. Hacemos lo mismo. 1º Trazamos un plano perpendicular a R que contiene a A, (como es una recta horizontal, el plano es proyectante horizontal). El plano corta a R en E. La distancia es AE y podemos conseguir la verdadera magnitud por diferencia de cota.
4. Este es igual, pero primero hemos tenido que hallar las trazas del plano formado por R y E.5. 1º Trazamos un plano perpendicular a R que contiene a A. Para ello nos valemos de una recta horizontal. 2º Hallamos la intersección de R con el plano (usamos un plano, Q, que contiene a R), es el punto E. 3º La distancia es el segmento AE. 4º Por diferencia de cotas conseguimos la verdadera magnitud de la distancia.6. Lo resolvemos de la misma manera que el caso anterior.
2. En este caso la recta es perpendicular al perfil, así que allí podemos ver directamente las distancias.3. Hacemos lo mismo. 1º Trazamos un plano perpendicular a R que contiene a A, (como es una recta horizontal, el plano es proyectante horizontal). El plano corta a R en E. La distancia es AE y podemos conseguir la verdadera magnitud por diferencia de cota.
4. Este es igual, pero primero hemos tenido que hallar las trazas del plano formado por R y E.5. 1º Trazamos un plano perpendicular a R que contiene a A. Para ello nos valemos de una recta horizontal. 2º Hallamos la intersección de R con el plano (usamos un plano, Q, que contiene a R), es el punto E. 3º La distancia es el segmento AE. 4º Por diferencia de cotas conseguimos la verdadera magnitud de la distancia.6. Lo resolvemos de la misma manera que el caso anterior.
solución FICHA 40
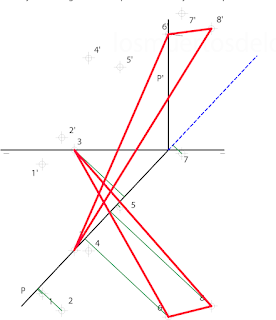
7.2º Trazamos un plano (M) que contiene a R para hallar la intersección de R con los planos7.3º. Hallamos la intersección de M con los planos, rectas S y T (son paralelas entre sí). Donde cortan a R conseguimos los puntos A y E,(intersección de R con los planos P y Q)7.4º. El segmento AE es la distancia entre los planos. Por diferencia de cotas podemos hallar la verdadera magnitud.8. 1º Elegimos un punto (A) que pertenezca a Q (vale cualquiera, así que usamos uno de una traza). Por A dibujamos una recta R perpendicular a Q.2º Medimos 20mm en la recta. No podemos hacerlo directamente, así que usamos la diferencia de cotas (Hemos usado un punto cualquiera (X)-hallado la verdadera magnitud de AX y sobre esta medir 20mm-trazando un segmento paralelo a la diferencia de cotas hallamos e), conseguido un punto e hallamos e'. El punto E está a 20 mm de distancia de A, aunque no lo parezca.
3º . Usando una recta horizontal (o frontal) trazamos un plano P paralelo a Q que contiene al punto E.4º Por supuesto la distancia es 20 mm, aunque parezca mayor.
41 Distancias V 1
1 . Al ser dos planos perpendiculares al PV se ve la distancia directamente2. La distancia se ve directamente al ser dos planos frontales.3. Son dos planos proyectantes y se ve directamente.4. P es un plano proyectante vertical , así que la solución se puede hacer directamente.5. Al ser perpendiculares al plano de perfil, se ve directamente la distancia en este.6, En el perfil podemos resolverlo directamente7. 1º Trazamos una recta (R) perpendicular a los planos 7.2º Trazamos un plano (M) que contiene a R para hallar la intersección de R con los planos7.3º. Hallamos la intersección de M con los planos, rectas S y T (son paralelas entre sí). Donde cortan a R conseguimos los puntos A y E,(intersección de R con los planos P y Q)7.4º. El segmento AE es la distancia entre los planos. Por diferencia de cotas podemos hallar la verdadera magnitud.8. 1º Elegimos un punto (A) que pertenezca a Q (vale cualquiera, así que usamos uno de una traza). Por A dibujamos una recta R perpendicular a Q.2º Medimos 20mm en la recta. No podemos hacerlo directamente, así que usamos la diferencia de cotas (Hemos usado un punto cualquiera (X)-hallado la verdadera magnitud de AX y sobre esta medir 20mm-trazando un segmento paralelo a la diferencia de cotas hallamos e), conseguido un punto e hallamos e'. El punto E está a 20 mm de distancia de A, aunque no lo parezca.
3º . Usando una recta horizontal (o frontal) trazamos un plano P paralelo a Q que contiene al punto E.4º Por supuesto la distancia es 20 mm, aunque parezca mayor.
SOLUCIÓN FICHA 41
42Distancias VI
SOLUCIÓN
1 Para hallar la distancia entre 2 rectas paralelas podemos trazar un plano perpendicular a éstas.Así que 1º Trazamos un plano P, perpendicular a R y S 2º Hallamos la intersección de las rectas con P (se ve directamente al ser un plano proyectante), obteniendo los puntos A y E. El segmento AE es la distancia. 3º Como l verdadera magnitud no se ve directamente, usamos la diferencia de cotas.
2 Lo resolvemos igual que en el caso anterior. Incluso nos hemos saltado el paso de dibujar las trazas del plano y hemos dibujado una recta perpendicular a s´y r´directamente.3 En este caso se ve directamente la distancia en el perfil.4 Este ejercicio lo podemos resolver también en el perfil. 1º Dibujamos la proyección s'' y la traza P´´ en el perfil. 2º Dibujamos un arco de 25 mm para hallar r'' 3º Trazamos r´y r.5 Podemos hacer los mismos pasos que en el primer ejercicio. Pero ahora es mas complicado al ser rectas oblícuas.1º Trazamos un plano, P, perpendicular a las rectas 2º Hallamos la intersección de R y S con P (puntos A y E), para ello hemos utilizado unos planos proyectantes auxiliares M y N.
3º El segmento AE es la distancia. Por diferencia de cotas hallamos la verdadera magnitud.
6 Hacemos los mismos pasos quq en los casos anteriores.2 Lo resolvemos igual que en el caso anterior. Incluso nos hemos saltado el paso de dibujar las trazas del plano y hemos dibujado una recta perpendicular a s´y r´directamente.3 En este caso se ve directamente la distancia en el perfil.4 Este ejercicio lo podemos resolver también en el perfil. 1º Dibujamos la proyección s'' y la traza P´´ en el perfil. 2º Dibujamos un arco de 25 mm para hallar r'' 3º Trazamos r´y r.5 Podemos hacer los mismos pasos que en el primer ejercicio. Pero ahora es mas complicado al ser rectas oblícuas.1º Trazamos un plano, P, perpendicular a las rectas 2º Hallamos la intersección de R y S con P (puntos A y E), para ello hemos utilizado unos planos proyectantes auxiliares M y N.
3º El segmento AE es la distancia. Por diferencia de cotas hallamos la verdadera magnitud.























































No hay comentarios:
Publicar un comentario