Homología selectividad 2025

Ejercicio en PDF

Examen completo  

SOLUCIÓN

1 Unimos A con A'. Al ser ortogonal, el eje es perpendicular a esta dirección y pasa por el punto doble C=C'

2. Uniendo A´con el punto doble del eje hallamos B'. Este se encuentra en una recta perpendicular al eje ( al ser afín todos los puntos estarán en rectas paralelas a esta dirección)

3. He empezado hallando un vértice D del triángulo interior: La recta que pasa por Ay D se corta en el eje con la que pasa por D' y A'.

4.  De igual manera hallamos los dos puntos restantes. Los lados de este triángulo interior son paralelos a los del triángulo exterior.

5 Repasamos la solución

examen diédrico selectividad junio 2025 Andalucía

 

SOLUCIÓN      

1. Dibujamos la proyección horizontal, trazando las diagonales al cuadrado

  2. Para hallar la altura podemos ver que se formaría un triángulo rectángulo , siendo la hipotenusa la arista, y un cateto la mitad de la altura.

  Así que tras hallar e ( en la LT) , conseguimos f con la medida de la diagonal del cuadrado. En la mitad estará la proyección vertical del cuadrado y las proyecciones del resto de puntos

3   Unimos cuidando distinguir entre aristas vistas y ocultas.

4  Para hallar la proyección de R he optado por hacer un abatimiento: 1º dibujamos (R) abatida , que forma 30 º con r. 2º hallamos (V) 3º desabatimos V, consiguiendo v' y la proyección v'.

También lo podemos hacer fácilmente usando un cambio de plano. Cambiando el P.V. para que sea paralelo a P.

5. Dibujamos las proyecciones de S, que son paralelas a las proyecciones de R.

Página de Guillermo Ortega

Una página muy recomendable para ver exámenes antiguos planteados y corregidos es la del profesor Guillermo Ortega, de la universidad de Huelva.

Enlace para ver exámenes anteriores

Enlace para ver exámenes resueltos
 

NORMALIZACIÓN 1-2ºBachillerato

Durante el curso hemos alternado los ejercicios de diédrico con otros de vistas normalizadas, Ahora vamos a profundizar en el tema de normalización, haciendo hincapié en vistas, secciones y cortes, escalas y acotación.
 Esta ficha son vistas de piezas inspiradas en algunas de las que han caido en selectividad en los últimos años.
Recordad que tenéis que poner tambien líneas discontínuas y ejes

Ficha en PDF

SOLUCIÓN

.

FICHA 2

perspectiva isométrica Selectividad Andalucía 2020

 

Ficha en PDF              

SOLUCIÓN       

1.Podemos dibujar un   croquis rápido, si no estamos seguros de ver la pieza.

   

 2. Para empezar a dibujarlo  calculamos la escala. La realidad es más grande que el dibujo, así que para ver cuando mide la realidad multiplicamos por 5 y dividimos por 3. La tenemos que dibujar a la misma escala, así que solo nos falta aplicar el coeficiente de reducción . ( para hallar C solo se usa la escala 3:5).

3.  Podemos empezar dibujando la planta ( a escala y con coeficiente). Ten en cuenta que se repiten muchas medidas.

4   

5  Trazamos recta verticales (paralelas a Z). Si tenemos clara la figura las podemos hacer más o menos altas.

6   Llevamos la altura sobre estas rectas y vamos dibujando caras. Las podemos llevar incluso con el compás si ya la hemos dibujado antes.

 

7  

8 

9 

10  Repasamos la solución. 

 

Normalización 1-4 1º Bachillerato

Normalización I

   En este ejercicio tiene que dibujar 3 vistas de piezas. Están inspiradas en algunas que han caído en selectividad. Los huecos son pasantes, es decir, tienes que imaginar que llegan hasta el final.

   Ficha en PDF      

SOLUCIÓN    

NORMALIZACIÓN  II      

Imprime ficha en PDF


SOLUCIÓN

NORMALIZACIÓN III

     

Ficha 3 en PDF       

SOLUCIÓN  

NORMALIZACIÓN IV

Ficha en PDF

SOLUCIÓN

P. isométrica selectividad junio 2018

 PERSPECTIVA ISOMÉTRICA IX

Ficha en PDF
SOLUCIÓN
<iframe width="560" height="315" src="https://www.youtube.com/embed/5IanhoZdh1U" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

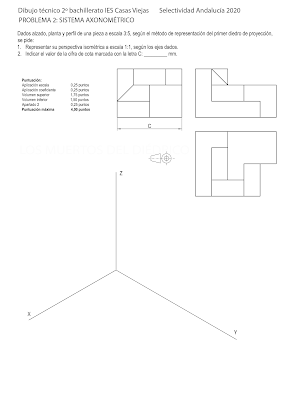
1º Empezamos haciendo un pequeño croquis de la pieza

2ºNos planteamos la escala: es 1:2, es decir, el dibujo que tenemos es la mitad que el real. Como lo tenemos que dibujar a escala 1:1, tendremos que multiplicar por 2 las medidas. Pero además es una perspectiva isométrica, así que tenemos que usar un coeficiente reductor de 0'816. Hay que multiplicar po2 2 y por 0´816.
Tenemos dos posibilidades, usar una calculadora (creo que es la mas fácil, y en selectividad lo permiten) o hacer una escala gráfica usando el teorema de Thales. Yo he usado la calculadora.En cualquer caso no es complicado, ya que se repiten muchas medidas.

3º Empezamos el dibujo. Yo me lo he planteado como si construyera un edificio y he empezado dibujando la planta

Trazamos semirectas verticales , as hacemos finas y claras, intentando no hacer innecesarias y que no nos falte ninguna.

Empezamos a trazar caras. Podemos ir cara por cara (tardaremos más pero es más difícil que nos equivoquemos) o ir haciendo todas las líneas paeelelas en una sóla pasada. Yo he empezado por la primera cara que vemos en el alzado, es muy clara y tiene que ser vertical.

Trazo la "L" que se ve en el perfil, y la cara horizontal que funcionaría como "azotea".

Dibujo la rampa

La pieza está ya clara y empiezo a repasar la figura. Para tardar menos, repaso de una sóla pasada todas las líneas paralelas.

Acabo de repasar, ten en cuenta que ahora se ve una cara en el "pasillo". No olvides las líneas ocultas.

Para acabar, colocamos la medida del segmento C. Recordad que tenemos que poner la real, así que multiplicamos por dos la del dibujo (60 mm, en mi caso)