Selectividad Andalucía 2019 IMPRESO-DIBUJO-EXTRA-TITULAR : SISTEMA DIÉDRICO

 IMPRESO-DIBUJO-EXTRA-TITULAR 

Examen en PDF

SOLUCION (es)      

1  Con centro en o hacemos una circunferencia para dibujar el hexágono. La dividimos en 6 partes usando el radio. Como 2 lados han de ser paralelos a la LT, dibujamos por o un segmento paralelo a la LT y situamos 2 vértices donde corte a la circunferencia.

 

2.  1. Dibujamos el hexágono: Las cotas de los 6 vértices se sitúan en la LT.  La altura la vemos directamente en el alzado. Trazamos las aristas (todas son vistas)

3. Como la base pertenece al plano horizontal, vemos directamente donde el plano corta al hexágono: Puntos A y B.

 

Vemos que el plano no puede cortar a las dos aristas delanteras, en cambio, ha de cortar a las otras 4.

¿Como hallar estos 4 puntos? tenemos varias opciones, paro las más fáciles quizá sean por cambio de planos o por intersección de recta y planos. Vamos a verlas

1- POR CAMBIO DE PLANOS

1 Cambiamos el plano vertical hasta ponerlo proyectante (No nos conviene que se mueva el horizontal)

 

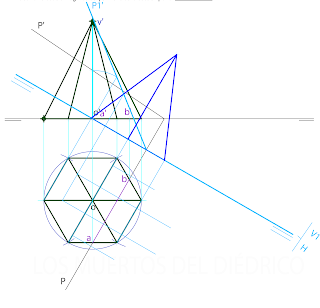
La nueva traza P1' la hallamos con una traza V y hallamos las nuevas proyecciones de la pirámide (las cotas no han cambiado)

2 En el alzado vemos donde corta a la pirámide (puntos C, D, E y F). Cuando tenemos las cotas (C1' por ejemplo) hallamos sus alejamientos (C), y, con estos sus cotas (C').  Con C y F, ho hay problema. Pero con C y D no basta con hacer una recta perpendicular a la nueva LT.

 

 Para hallar c' y d' llevamos las cotas sobre el alzado y una vez tengamos estas hallamos sus alejamientos

 Uniendo los 6 puntos obtenemos el corte. Para hallar la verdadera magnitud abatimos el plano (puedes usar P' o P1', pero es mucho más fácil abatir el proyectante.

Finalmente sumamos el perímetro.

2-POR INTERSECCIÓN DE RECTAS Y PLANO

 1.Hay dos aristas que podemos "meterlas" en un plano proyectante horizontal Q. La intersección de P y Q es una recta R, horizontal , donde corte a las aristas obtenemos los puntos C y D.

2. Dibujamos otro plano que contiene a otra arista. Sale una recta S, frontal, que nos permite hallar el punto E. Fíjate que podríamos dibujar la recta frontal directamente. Además, veo que el punto que falta , F, debería de estar a la misma cota.

3. Aún así, puede meter la arista que me falta en otro plano . Obtenemos una recta oblícua. Donde corta a la arista obtenemos el punto F. Fíjate que E y F formarían una recta horizontal del plano.

 

4  Unimos los puntos para hallar la sección. Por abatimiento hallamos la verdadera magnitud. Sumamos las aristas de la solución para hallar el perímetro