10 HOMOLOGÍA I

 Ficha 10 en PDF

 

ficha 9 ficha 11

SOLUCIÓN

Una homología se produce entre infinitos puntos de un plano con otros (infinitos de otro plano) cuando se cumple: 1que cada punto está unido con su homólogo y otro punto, llamado centro 2- Que las recta homólogas entre sí se cortan en otra recta , llamada eje.

Una homología AFÍN es similar, pero en este caso el centro estaría en el infinito, y por tanto las rectas son paralelas

Hay ejemplo de homología en nuestro entorno. Si encendemos una bombilla, esta sería en centro de una homología. Nuestra sombra sería homóloga de nuestra forma.

Cuando la luz está tan lejos que los rayos son paralelos se produciría una homología afín. Que espero pronto podáis experimentar en la playa.

Nuestro ojo o una cámara fotográfica es una máquina de hacer homologías: Lo que vemos es homólogo de la realidad

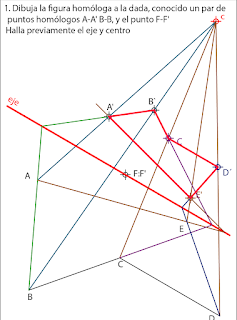
1 1 unimos los puntos con el centro 2-Unimos A con E en una recta, donde corte al eje , lo unimos con A' y obtenemos E'

 Trazando rectas que pasan por los puntos hasta el eje, vamos hallando el resto de puntos.

2   Uniendo los pares de puntos homólogos hallamos el centro 2- alargando las rectas AB y A'B' obtenemos un punto del eje. Lo unimos con  F:F' que también pertenece al eje.

Uniendo los puntos hasta el eje hallamos más homólogos.

3    1. En este caso empezamos haciendo paralelas por los vértices 2 Empezamos a hallar puntos. Recuerda que no sólo nos valemos de los lados del hexágono. En este caso he usado la recta AC, que aunque no sea un lado de la figura, también pertenece al plano de la homología.

 El punto donde la recta CD corta al eje es  homólogo de sí mismo, así que por ahí pasará C'D'.

4   1- Hacemos rectas paralelas a AA' que pasen por los vértices. Como el segmento AB es paralelo al eje, A'B' también lo será (se cortan con el eje en el infinito, eso dicen)

 Para hallar C' se ha usado la recta AC, ya que BC se corta fuera