Selectividad - Junio 21 DIÉDRICO

Hexaedro seccionado 

Ficha en PDF

SOLUCIÓN

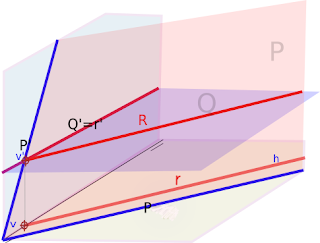
1 Alargando el segmento obtenemos la traza V de la recta. El plano tiene su traza P' en v' y P en a, ya que observamos que está situado en el plano horizontal.

2  Como el plano no es paralelo a ninguno de proyección, abatimos P con el segmento AB. Para ello nos valemos de su proyección en el plano de perfil. (La distancia entre P' y P la vemos en el perfil. A no se mueve y la traza V la llevamos a la traza P' abatida)

3 Usando el segmento AB abatido dibujamos el cuadrado, hallando los vértices Cy D. Hay dos posibles soluciones, pero descartamos la que se situa a la derecha, ya que se nos saldría del primer diedro.

    Des-abatimos el plano con los puntos C y D. A los dos se les ha situado en una recta M. Los lados del cuadrado se siguen viendo paralelos.

4. De los vértices del cuadrado trazamos rectas perpendiculares a las trazas de P. Hallamos un punto (g) del cuadrado superior, para ello nos valemos del perfil, donde se ve la arista CG del cubo en verdadera magnitud. la cota g' es igual a la de g'' y el alejamiento g lo vemos en el perfil.

5  Haciendo paralelas hallamos el resto de las aristas del hexaedro. Los lados del cuadrado de arriba son paralelos a los de abajo. 

6  Distinguimos entre aristas vistas y ocultas. 

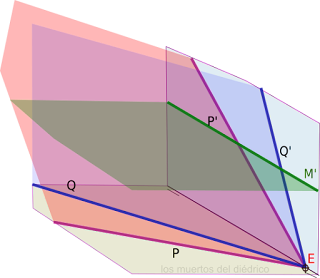
7  El plano Q solo tiene una traza que coincide con r'. El corte en el alzado se ve claramente (puntos 1-2-3-4 y 5). Los alejamientos los hallamos con rectas perpendiculares a la L.T. El alejamiento 1 nos coincide y no se ve directamente, así que dibujamos en el perfil la arista que parte de d y conseguimos el alejamiento de 1.Los puntos 3 y 4 están en el cuadrado superior y 2 y 5 en el inferior.

9  Uniendo los puntos hallamos la sección.

10 Finalmente medimos la diagonal de la cara. Esta la vemos en el cuadrado abatido. ( A mi me sale 59,1 mm , pero es posible que varíe algo al imprimir)

Sistema diédrico- Cilindro seccionado

 Selectividad Andalucía 2019

Ficha en PDF

SOLUCIÓN

El plano lo podemos dibujar usando el perfil. Al contener una recta paralela a la L.T. ha de ser paralelo a ésta.

La base del cilindro ha de ser una circunferencia tangente a la traza P y su alzado un rectángulo de 60 mm de alto.

La sección la podemos hallar dibujando el cilindro en el perfil (se ve como un rectángulo). El corte ha de ser una elipse; que se va a ver en el planta como un círculo. Para resolver la vista vertical vamos llevando puntos. Hay cuatro que son especialmente importantes (1-2-3-4), ya que coincidirían con los ejes de la elipse. El punto 4 está en la traza P y sería un extremo del eje mayor.1 sería el otro extremo.

  Los puntos 2 y 3 definirán el eje menor, sus alejamientos coinciden con un diámetro de la circunferencia-base y sus cotas están en la mitad de la sección.

Para acabar de hallar la proyección vertical hemos buscado otros cuatro puntos (5-6-7-8). Sus alejamientos se han situado en diámetros que forman 45º con los anteriores, de esta manera ahorramos líneas, ya que, por ejemplo, 5' y 6' estarán en una misma recta desde  la planta; o 6' y 7' a la misma cota. Fíjate que el dibujo es simétrico, lo que nos puede ahorrar también trabajo.

Para conseguir la verdadera magnitud podemos abatir el plano. usamos la traza P como charnela y situamos P' a una distancia que vemos en el perfil. 

Fíjate, también, que la base (circunferencia) es afín de la elipse, siendo la traza P el eje. Los puntos  7 - 5 y (7) -(5) son  afines.

Examen 1º bachillerato- Hasta intersección planos.

 

Ficha en PDF

Intersección II (1º bachillerato)

 

Ficha en PDF

SOLUCIÓN

1.  en este caso no tenemos ninguna traza, pero al no ser paralelos los planos ha de haber una solución. En el perfil podemos ver que se trata de una recta paralela a la L.T.

2    Este ejercicio lo podemos resolver también en el perfil

3     También lo vemos en el perfil. El plano P es un poco más complicado de dibujar porque la traza P es negativa.

4   Lo resolvemos hallando las trazas V y H, que se encuentran en la intersección de las trazas de los planos. Como el plano Q es proyectante, r' coincide con Q'.

5    Solo podemos obtener una traza H, eso quiere decir que no corta al P.V. Si nos imaginamos los planos vemos que es una recta frontal.

6. En este caso no hay ninguna traza, pero al imaginar los planos vemos que las proyecciones de las rectas coinciden con las trazas de los planos (es como la intersección de una pared con un techo)

7    Estos dos plano no son paralelos y, por tanto, han de cortarse. Pero vemos solo un punto de corte (E), donde se situarían también las trazas V y H . Pero necesitaríamos otro punto, al menos, para encontrar la solución.

En estos casos vamos a dibujar un plano auxiliar (M) que corta a P y Q. Vale cualquier plano, pero los horizontales o frontales son los más fáciles, ya que nos darían rectas horizontales o frontales.

Vemos que el plano M corta a P en una recta S y a Q en otra M, siendo las dos rectas horizontales. Estas se cortan en un punto A, que pertenece a las dos rectas y, por tanto, a los dos planos.

Uniendo E con A obtenemos la solución
 

8   En este caso obtenemos fácilmente la traza V. Pero vemos que las trazas P y Q se cortan fuera del papel . Tras descartar que sea error del profesor, que, como sabemos, no se equivoca nunca. Podemos optar por hacer el ejercicio en la mesa o pegando un papel a continuación. Pero sabemos que NO son métodos validos. Así que...

...No nos queda más remedio que usar un plano auxiliar, como en el ejercicio anterior. En este caso se ha utilizado un plano frontal que corta a P y Q en dos rectas frontales S y M.

Las rectas S y M se cortan en un punto A, que pertenece a P y Q, y, por tanto, a la recta intersección.

Uniendo el punto V con A obtenemos la recta intersección R.

Intersección de planos I (1º bachillerato)

 

Ficha en PDF

soluciones

La intersección de dos planos va a ser una recta. Todos los puntos de ésta pertenecerán a ambos planos. Para hallar las proyecciones de la recta vemos donde se cortan las trazas de los planos. Las trazas V y H de la recta estarán donde se corten las de los planos.

1.

2.

3

4

5 En este caso solo podemos obtener una traza V. P y Q son paralelas. Si nos imaginamos los planos la intersección ha de ser una recta de punta.

6

7 En este caso tampoco tenemos una traza H, pero vemos que la intersección ha de ser una recta horizontal.

 

8