Intersección II (1º bachillerato)

 

Ficha en PDF

SOLUCIÓN

1.  en este caso no tenemos ninguna traza, pero al no ser paralelos los planos ha de haber una solución. En el perfil podemos ver que se trata de una recta paralela a la L.T.

2    Este ejercicio lo podemos resolver también en el perfil

3     También lo vemos en el perfil. El plano P es un poco más complicado de dibujar porque la traza P es negativa.

4   Lo resolvemos hallando las trazas V y H, que se encuentran en la intersección de las trazas de los planos. Como el plano Q es proyectante, r' coincide con Q'.

5    Solo podemos obtener una traza H, eso quiere decir que no corta al P.V. Si nos imaginamos los planos vemos que es una recta frontal.

6. En este caso no hay ninguna traza, pero al imaginar los planos vemos que las proyecciones de las rectas coinciden con las trazas de los planos (es como la intersección de una pared con un techo)

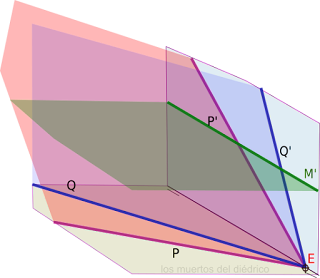
7    Estos dos plano no son paralelos y, por tanto, han de cortarse. Pero vemos solo un punto de corte (E), donde se situarían también las trazas V y H . Pero necesitaríamos otro punto, al menos, para encontrar la solución.

En estos casos vamos a dibujar un plano auxiliar (M) que corta a P y Q. Vale cualquier plano, pero los horizontales o frontales son los más fáciles, ya que nos darían rectas horizontales o frontales.

Vemos que el plano M corta a P en una recta S y a Q en otra M, siendo las dos rectas horizontales. Estas se cortan en un punto A, que pertenece a las dos rectas y, por tanto, a los dos planos.

Uniendo E con A obtenemos la solución
 

8   En este caso obtenemos fácilmente la traza V. Pero vemos que las trazas P y Q se cortan fuera del papel . Tras descartar que sea error del profesor, que, como sabemos, no se equivoca nunca. Podemos optar por hacer el ejercicio en la mesa o pegando un papel a continuación. Pero sabemos que NO son métodos validos. Así que...

...No nos queda más remedio que usar un plano auxiliar, como en el ejercicio anterior. En este caso se ha utilizado un plano frontal que corta a P y Q en dos rectas frontales S y M.

Las rectas S y M se cortan en un punto A, que pertenece a P y Q, y, por tanto, a la recta intersección.

Uniendo el punto V con A obtenemos la recta intersección R.