Parábola dados foco, punto y recta tangente

Selectividad  suplente Andalucía Junio 2022

Examen en PDF

SOLUCIÓN

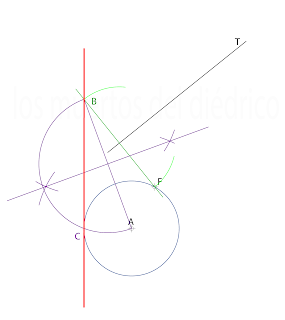
Este ejercicio es un poco "raro", no da los típicos datos para resolver una parábola así que para hallar la solución podemos empezar haciendo un pequeño croquis con la solución para intentar resolverlo.

1. Como la distancia de cada punto a la directriz ha de ser similar a la del foco, podemos empezar haciendo una circunferencia con centro en A y radio AF: la directriz ha de ser tangente a ésta.

2 Desde F trazamos una recta penpendicular a la tangente T. la distancia de la tangente al foco ha de ser igual a la distancia hasta la directriz : El punto B ha de estar en la directriz.

3. Dibujando una recta tangente a la circunferencia que pasa por B hallamos la directriz . (recuerda que , aunque se pueda hacer fácilmente colocando directamente la regla, hemos de utilizar el método correcto, hallando primero el punto de tangencia)

4.  Trazando una perpendicular a la directriz desde B hallamos el punto de tangencia P. Perpendicular a la recta tangente por el punto P obtenemos la normal.

5,  El eje lo conseguimos con una perpendicular a la directriz desde F. En la mitad de la distancia entre F y la directriz estará el vértice.

6  Finalmente dibujamos la parábola. Para ello vamos trazando rectas paralelas a la directriz, medimos con el compás la distancia hasta la directriz y haciendo centro en el foco vamos hallando puntos: Se tiene que cumplir que cada punto está igual de lejos de la directriz y del foco.  Cuando tengamos bastantes puntos , dibujamos la cónica a mano alzada.

Aquí puedes descargar más exámenes de selectividad.