13 HOMOLOGÍA IV
Ficha 13 en PDFSOLUCIÓN
1 1 Dibujamos la circunferencia inscrita en el cuadrado (el radio lo conseguimos con un segmento perpendicular al lado). 1.2. Uniendo Q con Q1 obtenemos la dirección de la afinidad. `Dibujamos desde C y D rectas paralelas a la dirección. 1.3 Trazando rectas desde los puntos ( C y D) que pasen por Q hasta el eje, hallamos las rectas homólogas que nos permiten hallar los puntos afines. Fíjate que como el segmento CD es paralelo al eje, C'-D' también lo será. Uniendo los puntos obtenemos la figura afín al cuadrado.
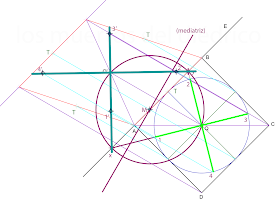
1. 2.1 Primero vamos a obtener los puntos de tangencia de la circunferencia con el cuadrado. Con rectas paralelas a la dirección obtenemos sus homólogos. Estos puntos pertenecerán a la elipse afín, pero no son los extremos de los ejes.1.3 Para hallar los ejes: 3.1. Trazamos la mediatriz al segmento Q-Q1. Donde ésta corte al eje obtenemos el punto M. 3.2. Con centro en M dibujamos una circunferencia que pase por Q y Q1. Donde corte al eje obtenemos dos puntos (X. e Y). 3.3. Unimos X e Y con Q y conseguimos dos diámetros de la circunferencias perpendiculares entre sí : 1-3 y 2-4. ( Si te das cuenta, hemos usado el arco capaz para 90º, que es un semicírculo)1. 4. Los ejes de la elipse serán los homólogos de los diámetros anteriores. Para hallarlos, unimos X e Y con Q1. para hallar los homólogos de los puntos 1,2,3 y 4 trazamos rectas paralelas a la dirección. 3', por ejemplo, estará en la recta que pasa por Q1 y es homólogo a la que corta en el eje a la que pasa por · y Q.Los segmentos 4'-2' y 1'-3' son los ejes de la elipse.











No hay comentarios:
Publicar un comentario