Son 4 ejercicios basados en problemas propuestos de selectividad.
SOLUCIÓN
1 1º Como todos los puntos están a la misma distancia del foco y de la recta directriz, podemos hacer circunferencias desde los puntos con radios hasta F. La recta directriz ha de ser una recta tangente a las dos circunferencias . 2º El eje ha de ser una recta perpendicular a la directriz que pasa por F. 3º El vértice es equidistante entre F y la directriz (lo podemos hallar con una mediatriz)
4º Vamos hallando puntos. Para ello: 1º trazamos rectas paralelas a la directriz. Haciendo centro en F trazamos circunferencias con radio desde la directriz a cada una de las paralelas. Donde se corten estarán los puntos de la parábola, ya que se cumple que la distancia de cada punto al foco y a la directriz es la misma.Unimos los puntos5º la tangente la hallamos trazando la bisectriz2 1º Trazamos una perpendicular desde A hasta la directriz. 2º el ángulo que obtenemos lo llevamos al otro lado 3º Dibujamos una circunferencia llevando la distancia entre A y la directriz y obtenemos el foco ( A tiene que estar a la misma distancia de la directriz y el foco) 4º Desde el foco trazamos una perpendicular a la directriz y obtenemos el eje. 5º el vértice estará a misma distancia de la directriz y el foco (lo podemos hallar con una mediatriz)6 º Dibujamos la parábola 7º la normal es perpendicular a la tangente en A.3 1ºTrazamos una recta que pase por los focos (ese será el eje transversal). 2º Dibujando la mediatriz de la distancia entre los focos hallaremos el otro eje (conjugado)
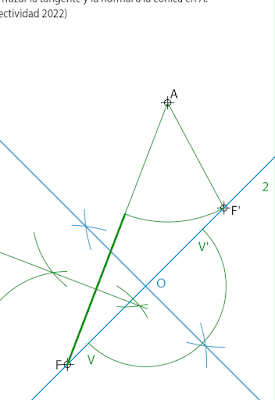
3º Unimos los focos al punto A. Si restamos al segmento AF el segmento AF' obtenemos la distancia entre los vértices.( se cumple que la diferencia de distancias de un punto a los focos es contante) 4º Trazamos una mediatriz, para dividir el segmento anterior por la mitad, y, con esta, obtenemos los vértices.
4º Vamos hallando puntos de la hipérbola. Para ello vamos situando puntos aleatoriamente en el eje (1,por ejemplo) Llevando la distancia de estos puntos a los vértices desde los focos hallamos puntos de la cónica.5º Unimos los puntos para dibujar la curva. 6º Para hallar la tangente, trazamos la bisectriz al ángulo entre AF y AF'.4 Trazamos rectas perpendiculares a las tangentes. Sobre estas, llevamos la distancia hasta el foco y obtenemos los puntos A y B. Al estar a la misma distancia, pertenecerán a la directriz. Unimos A y B, obteniendo la directriz. El eje lo dibujamos perpendicular a la directriz, pasando por F. El vértice estará en el punto medio entre F y la directriz.(lo podemos hallar trazando la mediatriz) Dibujando rectas perpendiculares a la directriz desde A y B obtenemos los puntos de tangencia. como no nos piden que dibujemos la cónica, NO la dibujamos.















No hay comentarios:
Publicar un comentario